Retourner à : Introduction à la programmation avec Blockly
Les voyages en train de font à un rythme prévisible : vous savez quand vous partez et vous avez quand vous arrivez, ce qui vous permet de savoir également pendant combien de temps vous allez voyager.
Dans ce défi, vous allez devoir créer un algorithme capable de calculer le temps de trajet d’un train connaissant son horaire (heure et minutes) de départ et son horaire (heure et minutes également) d’arrivée.
Un résultat possible à l’exécution de votre algorithme est le suivant :
Départ à 14h00 et arrivée à 15h16 :
Début de l'exécution → Durée du trajet : 1 heures et 16 minutes Fin de l'exécution
Départ à 15h30 et arrivée à 18h20 :
Début de l'exécution → Durée du trajet : 2 heures et 50 minutes Fin de l'exécution
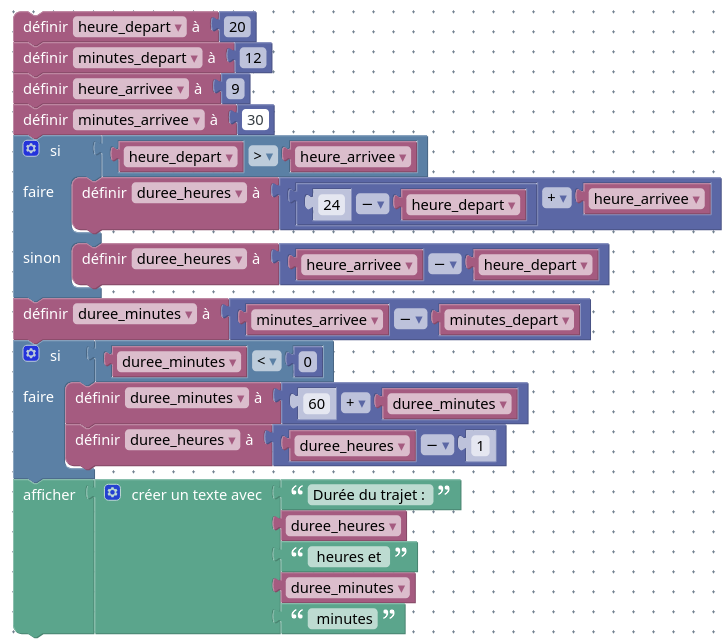
Départ à 20h12 et arrivée à 9h30 (c’est un train de nuit !) :
Début de l'exécution → Durée du trajet : 13 heures et 18 minutes Fin de l'exécution
Les 3 exemples ci-dessus sont les 3 cas que vous allez devoir gérer si vous souhaitez que votre algorithme puisse appréhender tous les cas de figure. Cependant, vous n’êtes pas obligé(e) de gérer le plus difficile (le troisième) dès que vous commencez, vous pouvez vous contenter du premier, qui est le plus simple, puis le modifier pour pouvoir gérer le second, et enfin le troisième.
Pour gérer le premier cas de figure, rien de plus simple : il suffit de soustraire l’heure d’arrivée à l’heure de départ et les minutes d’arrivée à l’heure d’arrivée, car dans les deux cas, la valeur d’arrivée est plus grande que la valeur de départ.
La gestion du second cas de figure requière d’ajouter une condition car la valeur des minutes d’arrivée est plus faible que la valeur des minutes de départ ! Dans ce cas il faut “reprendre” 60 minutes à une heure pour les intégrer dans le résultat.
Enfin, le troisième cas est le plus complexe puisque la valeur de l’heure d’arrivée est plus faible que les heures de départ… cette fois il faut “reprendre” 24h à une journée pour que ce cas de figure devienne simple à traiter. Au final, l’algorithme gérant tous les cas de figure est le suivant :