Retourner à : Introduction à la programmation avec Blockly
Un nombre premier est un nombre qui ne peut être divisé que par lui-même ou le chiffre 1 (par exemple, 5 est premier, mais 12 ne l’est pas).
Le but de cet exercice est de créer un algorithme qui va demander à l’utilisateur de fournir un nombre, et qui va ensuite indiquer s’il est premier ou non.
Voici un exemple de ce que peut donner votre rendu :
Début de l'exécution L'utilisateur a répondu "237" à la question "Choisissez un chiffre ou un nombre" → Le chiffre ou nombre n'est pas primaire Fin de l'exécution
Si un nombre premier ne peut être divisé que par 1 ou par lui-même, cela veut dire qu’il ne peut pas être divisé par d’autres nombres (j’enfonce une porte ouverte avec cette remarque !).
Si vous recherchez quels sont les nombres qui peuvent diviser votre nombre à tester, il faut considérer que les nombres 0 et 1 sont à exclure de vos hypothèses de division car on ne peut pas diviser par 0 et tous les nombres sont divisibles par 1. Le nombre lui-même est à exclure car tous les nombres sont divisibles pas eux-mêmes.
Ensuite, un nombre ne peut évidemment pas être divisé par un nombre plus grand que lui (13 ne peut pas être divisé par 26 car le résultat de la division de 13 par 26 est 0.5, ce n’est pas un nombre entier).
Cette indice devrait vous aider à lister tous les nombres que vous devez tester pour voir s’ils sont diviseurs du nombre de l’utilisateur. Il vous reste à trouver comment déterminer qu’un nombre peut être divisé par un autre grâce à un algorithme.
L’algorithme est le suivant :
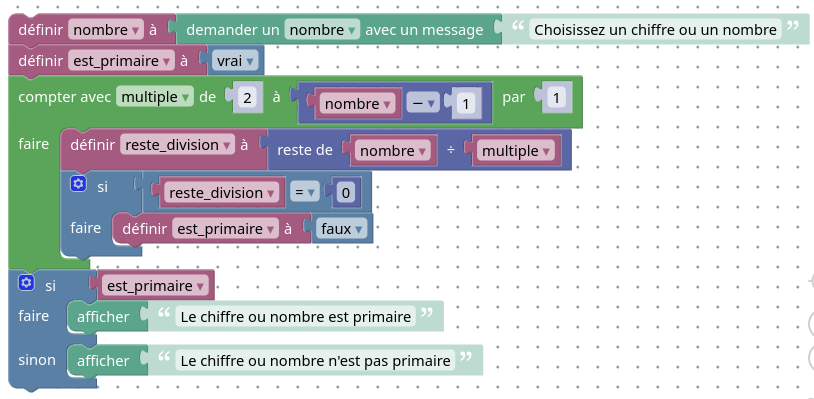
L’algorithme que je vous ai proposé est loin (très loin même) d’être efficace !
En effet, vous aurez remarqué qu’il va énumérer tous les nombres entre 2 et le nombre de l’utilisateur (minoré de 1)… si l’on exécute cet algorithme avec un chiffre pair, on se rend compte tout de suite qu’il effectue trop de calcul car le premier tour de boucle va indiquer immédiatement que le nombre est premier… mais il va tout de même faire tous les autres tours de boucle !
Ensuite, pour identifier un nombre premier, il ne sert à rien de tester tous les nombres qui lui sont inférieurs, on peut se contenter de tous les nombres inférieurs à sa racine carrée, ce qui réduit (drastiquement) le nombre de tours de boucles nécessaire.
Enfin, les grands nombres sont difficiles à identifier car il faut faire un grand nombre de tours de boucles. D’ailleurs, vous l’avez peut-être expérimenté par vous-même : l’éditeur Blockly du LCJ vous empêche, avec un tel algorithme, de traiter les grands nombres. En effet, pour prévenir les erreurs dans le code lors de l’exécution, le nombre de tours de boucles autorisé est limité, votre algorithme a donc peut-être été arrêté en cours d’exécution !